1. Curiosity Bottleneck: Exploration by Distilling Task-Specific Novelty

This post is an introduction to the paper "Curiosity Bottleneck: Exploration by Distilling Task-Specific Novelty" by Kim et al 1.
The paper deals with informative exploration method when task-irrelevant noise are present within the visual observation.
By distilling the informative from the uninformative, the agent is able to successfully ignore the distractive visual entities when making decision about choice of action or calculating the intrinsic reward for exploration.

2. Exploration in RL

Exploration vs. exploitation is a well known paradox in reinforcement learning.
A careful tradeoff between the two is required for the optimal performance of the learning algorithms.
Previous and recent algorithms attempted to achieve the balnace between the exploration and exploitation through counts 2,3, pseudo-counts 2,4,5, information gain 6,7, prediction error 8,9,10,11,12,13,14, or value-aware model prediction 15,16.
For example, a count based algorithm would keep track of each, or each type of the observation and use the inverse of the count as the novelty of a given state.
However, considering situations where we extend the task to real world applications, the obervation often includes noise and distraction irrelevant to solving the target task.
For example, imagine a robot navigation task through crowded street.
In order to succesffully navigate from point A to point B, details about the crowd passing by, such as color of the shirt, facial features, or gender, contain information irrelevant to the task of navigation.
However, these details may contain high visual information but no contextual information, in other words, they should be treated as distractions.
Also, change in those factors should not contribute to the agents decision about the measure of novelty of such states.
However, count based or prediction based algorithms fail to distinguish the informative and distractive observations, purely from the image only.
The unpredictive, never seen, changes in the visual input will increase the novelty of the observation, mis-guiding the agent to explore in the unecessary direction.
The resulting behavior would be an agent stuck in a local optima or severly inefficient learning speed.
Such behavior is well deomnstrated through "Noisy-TV problem" 17.

Noisy-tv agent image from video by Deepak Pathak (image taken from Google AI blog source

---

In order to overcome these problems, the agent must learn to differentiate the valuable information from the noise.
As method to distinguishing those information, Curiosity Bottleneck (CB) applies the concept of information bottleneck (IB) principle 18,19,20,21,22,22.
By creating an auxiliary network which mimics the learned value function with latent Z space modeled as the information bottleneck, the auxiliary network learns to filter out the distractive information when learning the current value estimates of the states.

3. Information Bottleneck and Curiosity

The basic expression for information bottleneck consists of two mutual information terms as follows.

The first mutual information term represents how predictive latent space is about target prediction .
The second mutual information term is compressiveness of about the input space .
The expression as a whole means that we want to train a latent space to capture only the information necessary to predict while filtering out the unnecessary information from .
However, directly these terms cannot be directly calculated for the marginal distribution of is intractable.
And thus, CB approximates these terms as suggestsd by Alemi et al. (2017).
First, minimizing the upper bound of is equivalent to optimizing a standard supervised learning objective as below.

where is variational approximation of .
The entropy of the label will be ignored in the calculation becuase it is irrelevant to the optimization objective.
The second term, , is optimized by minimizing the upper bound, which comes out to be the KL-divergence between and , a variational approximation of .

Putting them all together, the final form of the loss function becomes,

and the KL term becomes the intrinsic reward for exploration.

4. Adaptive Exploration

One outstanding feature of CB is that it adaptively transitions from task-identification phase to task-specific exploration phase.
In general exploration algoroithms, a scene is novel if specific version of the scene as a whole is never seen to the agent, regardless of its context.
Here, the phase when all new scenes are treated equally novel before the agent learns to distinguish scenes by its context, is termed task-identification phase.
Minimizing the KL term results in decreasing the overall intrinsic reward of often-seen scenes.
however, as the agent experiences more rewards, the latent of already seen scenes with high distinguishable values are pushed away from the prior in order to make accurate prediction of the state value from , increasing the KL divergence of such states.
This phase, when the intrinsic rewards are governed by the value of the states, is called task-specific exploration.

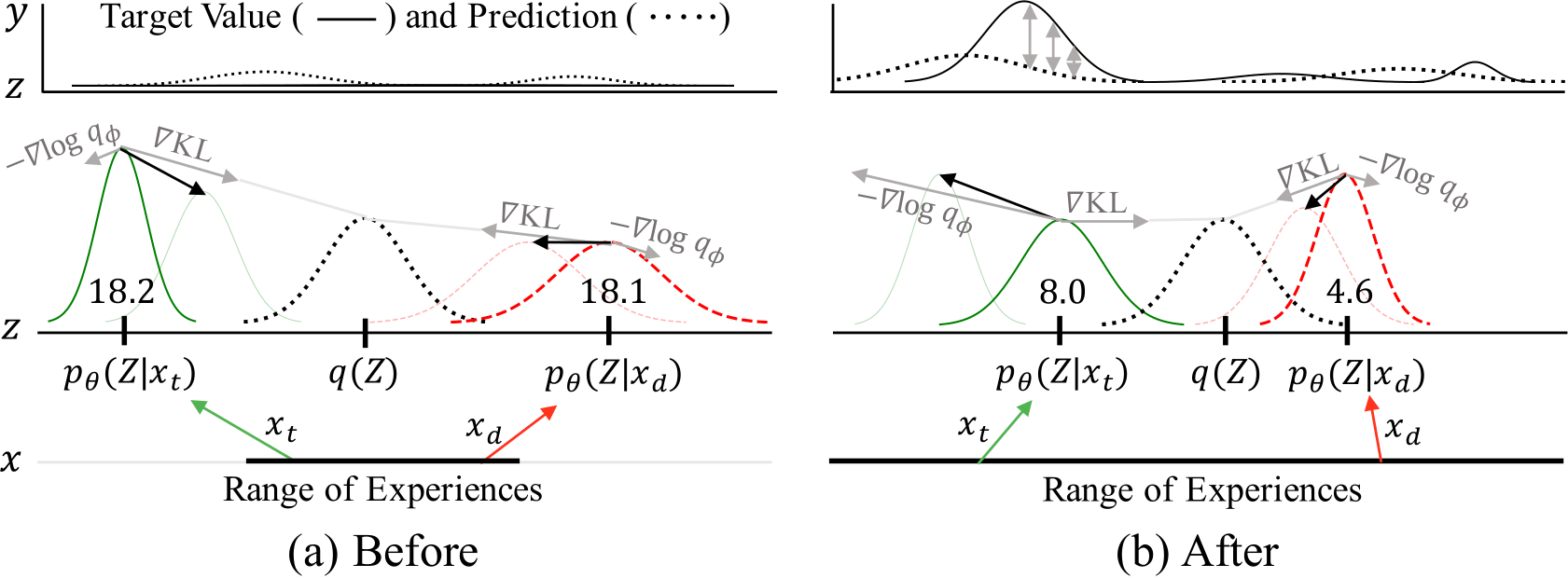
Diagram of adaptive exploration transition 1

This comparison between novelty by pure frequency and frequency conditioned on task is shown through classification of Fashion-MNIST 24 with intentionally added noise.

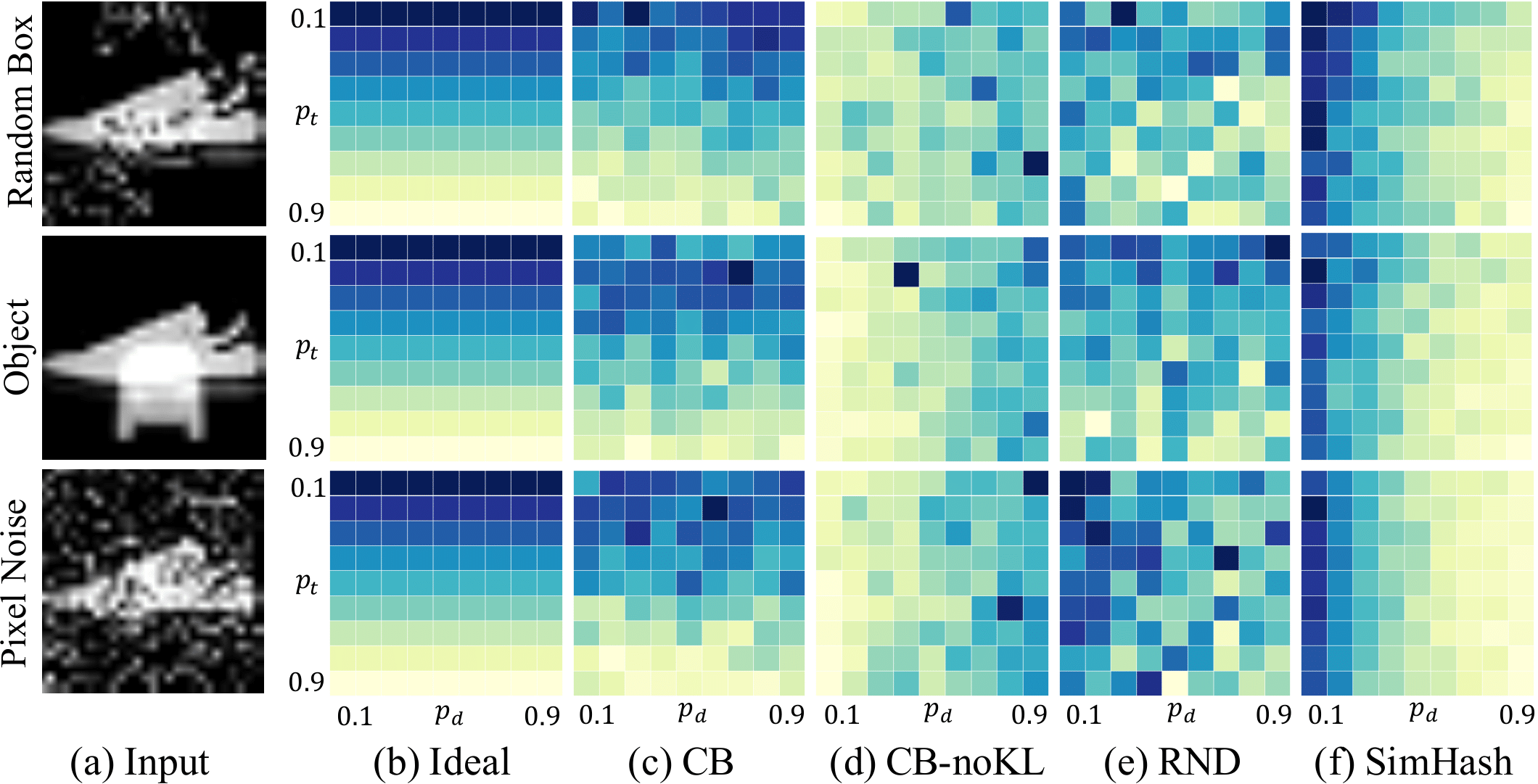
Result 1 of fashion-mnist 24 with added distraction

The y-axis of the graph is the retention ratio (how often the image of target label was shown) and the x-axis is the probability of the distraction appearing in image.
All distractions are randomly generated, in order to conserve visual novelty.
As mentioned several times, the frequency of the image shown should affect the novelty of the(cite)On the other hand, ideally, the added distractions does not change the label of the image and thus not affect the calculated novelty.
This ideal situation is depicted in the second column (b) of the figure shown above.
However, if an algorithm fails to filter out the distraction, the novelty is affected by the random noise (become random) as shown in column (e).
On the other hand, CB successfully ignores the injected distractions and reproduces the ideally pattern as shown in column (c).
Besides the ability to successfully measure task-specific novelty, CB's ability to explore are shown through a custom made treasure-hunt task and few hard-exploration games of Atari.
(Gravitar, Montezuma's Revenge and Solaris, to name them.
Refer to the original paper for details on the tresure-hunt task.)

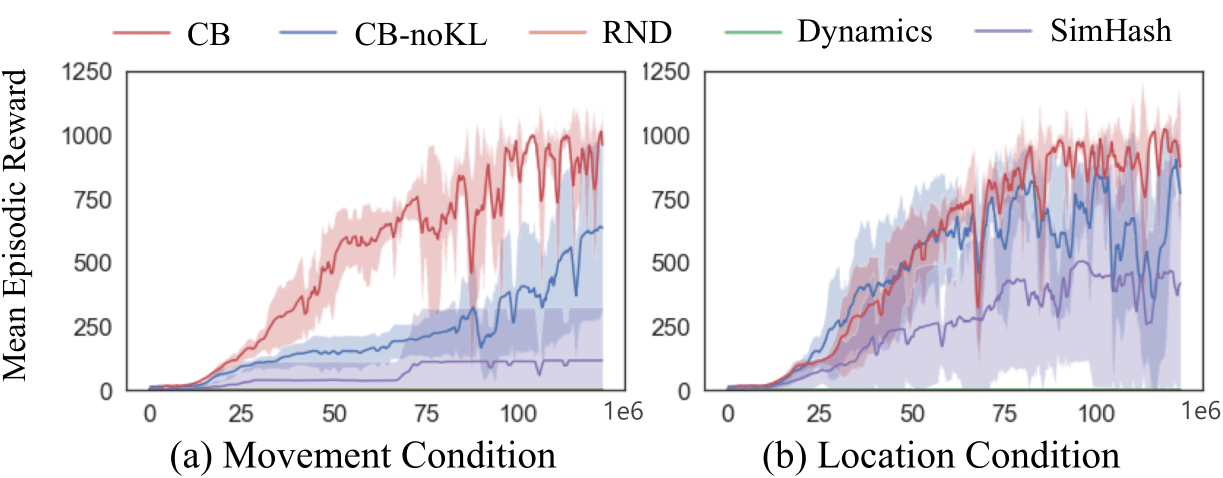
Performance graph in treasure-hunt 1

Performance graph of Atari tasks 1

5. Implementation

Algorithm of Curiosity-Bottlneck with PPO 25

Another convenient feature of CB is that it can be easilly implemented and used with various algorithms.
CB requires an auxiliary network, consisting of a compressor, a gaussian layer, and a value predictor.
The compressor, usually structured with convolutional layers, recieves image and produces mean and standard deviations of the posterior distributions.
Than, samples are passed into the predictor, normally MLP, to predict the value of the given sample.
Then, the intrinsic reward, the KL-divergence, is calculated from the distribution layer.
The overview of CB is shown in the figure from the paper.

Curiosity-Bottleneck Overview 1

6. Summary

There has been major advances in reinforcement learning with the combination with the deep learning.
However, the application of deep learning itself does not address the existing problems such as exploration.
Even the most succesfull algorithms such as DQN, DDPG, TRPO, and PPO depend on random stochaticity for exploration.
Other recent works that directly tackle the exploration problem, such as ICM and RND, demonstrate more sophisticated approach.
However, these works still have large potential to advance.
This paper suggests one of tyhe advances that can be made, by excluding the task-irrelevant noise when detecting the novelty of the state.

Reference

1

Kim, Y., Nam, W., Kim, H., Kim, J., and Kim, G. Curiosity-Bottleneck: Exploration by Distilling Task-Specific Novelty. In ICML, 2019

2

Bellemare, M. G., Srinivasan, S., Ostrovski, G., Schaul, T., Saxton, D., and Munos, R. Unifying count-based exploration and intrinsic motivation. In NeurIPS, 2016.

3

Ostrovski, G., Bellemare, M. G., van den Oord, A., and Munos, R. Count-based exploration with neural density models. In ICML, 2017.

4

Tang, H., Houthooft, R., Foote, D., Stooke, A., Chen, X., Duan, Y., Schulman, J., Turck, F. D., and Abbeel, P. #exploration: A study of count-based exploration for deep reinforcement learning. In NeurIPS, 2017.

5

Choi, J., Guo, Y., Moczulski, M., Oh, J., Wu, N., Norouzi, M., and Lee, H. Contingency-aware exploration in rein- forcement learning. In ICLR, 2019.

6

Houthooft, R., Chen, X., Duan, Y., Schulman, J., Turck, F. D., and Abbeel, P. VIME: variational information maximizing exploration. In NeurIPS, 2016.

7

Chen, R. Y., Sidor, S., Abbeel, P., and Schulman, J. UCB ex- ploration via Q-ensembles. CoRR, abs/1706.01502, 2017. URL http://arxiv.org/abs/1706.01502.

8

Schmidhuber, J. A possibility for implementing curiosity and boredom in model-building neural controllers. In Proc. of the international conference on simulation of adaptive behavior: From animals to animats, pp. 222– 227, 1991.

9

Stadie, B. C., Levine, S., and Abbeel, P. Incentivizing ex- ploration in reinforcement learning with deep predictive models. arXiv preprint arXiv:1507.00814, 2015. URL http://arxiv.org/abs/1507.00814.

10

Achiam, J. and Sastry, S. Surprise-based intrinsic motivation for deep reinforcement learning. NeurIPS DRL Workshop, 2016.

11

Pathak, D., Agrawal, P., Efros, A. A., and Darrell, T. Curiosity-driven exploration by self-supervised predic- tion. In ICML, 2017.

12

Haber, N., Mrowca, D., Wang, S., Li, F., and Yamins, D. L. Learning to play with intrinsically-motivated, self-aware agents. In NeurIPS, 2018.

13

Fox, L., Choshen, L., and Loewenstein, Y. DORA the explorer: Directed outreaching reinforcement action- selection. In ICLR, 2018.

14

Burda, Y., Edwards, H., Storkey, A., and Klimov, O. Explo- ration by random network distillation. In ICLR, 2019b.

15

Luo, Y., Xu, H., Li, Y., Tian, Y., Darrell, T., and Ma, T. Algo- rithmic framework for model-based deep reinforcement learning with theoretical guarantees. In ICLR, 2019.

16

Farahmand, A.-M., Barreto, A., and Nikovski, D. Value- aware loss function for model-based reinforcement learn- ing. In AIStats, 2017.

17

Burda, Y., Edwards, H., Pathak, D., Storkey, A., Darrell, T., and Efros, A. A. Large-scale study of curiosity-driven learning. In ICLR, 2019.

18

Tishby, N. and Zaslavsky, N. Deep learning and the infor- mation bottleneck principle. In IEEE Information Theory Workshop, 2015.

19

Shwartz-Ziv, R. and Tishby, N. Opening the black box of deep neural networks via information. arXiv preprint arXiv:1703.00810, 2017. URL http://arxiv.org/ abs/1703.00810.

20

Alemi, A. A., Fischer, I., Dillon, J. V., and Murphy, K. Deep variational information bottleneck. In ICLR, 2017.

21

Alemi, A. A. and Fischer, I. GILBO: one metric to measure them all. In NeurIPS, 2018.

22

Alemi, A. A., Fischer, I., and Dillon, J. V. Uncertainty in the variational information bottleneck. UAI UDL Workshop, 2018a.

23

Alemi, A. A., Poole, B., Fischer, I., Dillon, J. V., Saurous, R. A., and Murphy, K. Fixing a broken ELBO. In ICML, 2018b.

24

Xiao, H., Rasul, K., and Vollgraf, R. Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms. arXiv preprint arXiv:1708.07747, 2017. URL http://arxiv.org/abs/1708.07747.

25

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and Klimov, O. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347, 2017.
URL http://arxiv.org/abs/1707.06347